Welcome to rippleTank!¶
rippleTank is a simulator that aims to help students understand how waves behave on a ripple tank, as well as motivating the use of computational tools to solve physical problems. Fully written with Python, rippleTank depends on the following libraries:
Installing¶
rippleTank is freely available on PyPI, thus can be easily installed with pip:
pip install rippleTank
The development version is hosted on GitHub, and can be installed by running the setup.py.
python setup.py install
How it works¶
A wave is described by the wave equation:
\(\nabla^2\psi = \dfrac{1}{v^2}\dfrac{\partial \Psi}{\partial t} \qquad \text{where } v \text{ is the propagation speed}\)
In order to solve the differential equation, a finite difference scheme is used.
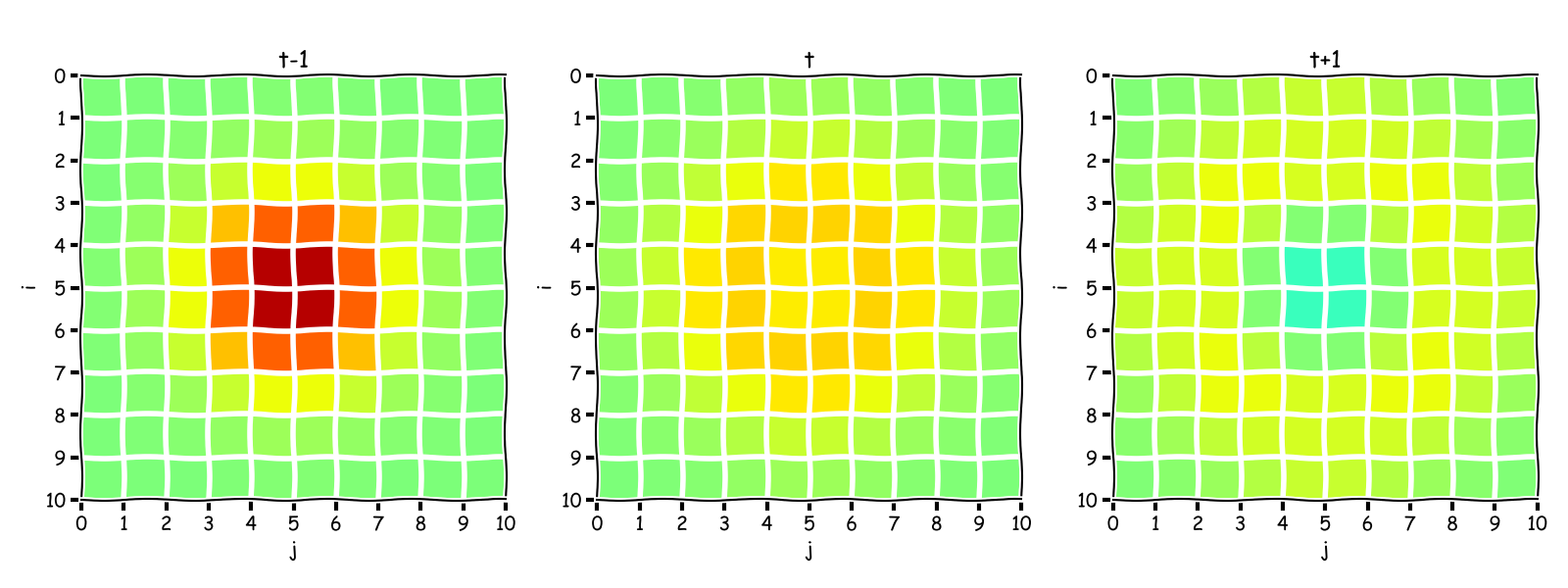
Space is discretized in n_cells_x and n_cells_y, each cell has a value of \(\Psi\) stored on a matrix. For every cell whose location is not a boundary:
\(\Psi^{t+1}_{i, j} = 2\Psi^{t}_{i, j} - \Psi^{t-1}_{i, j} + \left(\dfrac{v\Delta t}{\Delta x}\right)^2\left(\Psi^{t}_{i, j+1} -2\Psi^{t}_{i, j} + \Psi^{t}_{i, j-1}\right) + \left(\dfrac{v\Delta t}{\Delta y}\right)^2\left(\Psi^{t}_{i+1, j} -2\Psi^{t}_{i, j} + \Psi^{t}_{i-1, j}\right)\)
If the boundary is closed:
\(\Psi^{t+1}_{boundary, j} = \Psi^{t}_{boundary, j}\)
\(\Psi^{t+1}_{i, boundary} = \Psi^{t}_{i, boundary}\)
\(\Psi^{t+1}_{boundary, boundary} = \Psi^{t}_{boundary, boundary}\)
For an open boundary the following relations are applied:
\(\Psi^{t+1}_{i, 0}=\dfrac{v\Delta t}{\Delta x}\left(\Psi^t_{i, 1} - \Psi^t_{i, 0}\right) + \Psi^t_{i, 0}\)
\(\Psi^{t+1}_{0, j}=\dfrac{v\Delta t}{\Delta y}\left(\Psi^t_{1, j} - \Psi^t_{0, j}\right) + \Psi^t_{0, j}\)
\(\Psi^{t+1}_{i, \text{n_cells_x}-1}=\dfrac{v\Delta t}{\Delta x}\left(\Psi^t_{i, \text{n_cells_x}-1} - \Psi^t_{i, \text{n_cells_x}-2}\right) + \Psi^t_{i, \text{n_cells_x}-1}\)
\(\Psi^{t+1}_{\text{n_cells_y}-1, j}=\dfrac{v\Delta t}{\Delta y}\left(\Psi^t_{\text{n_cells_y}-1, j} - \Psi^t_{\text{n_cells_y}-2, j}\right) + \Psi^t_{\text{n_cells_y}-1, j}\)
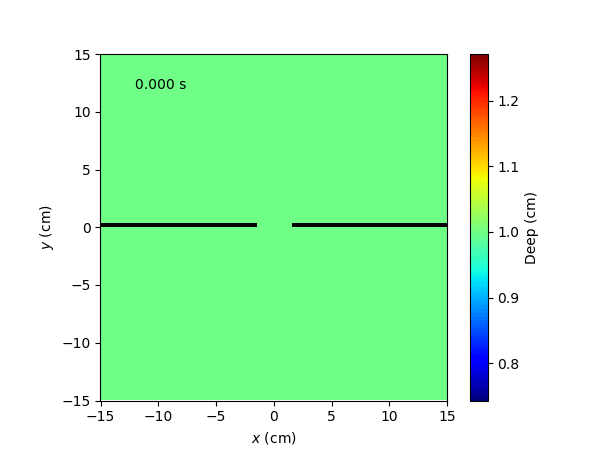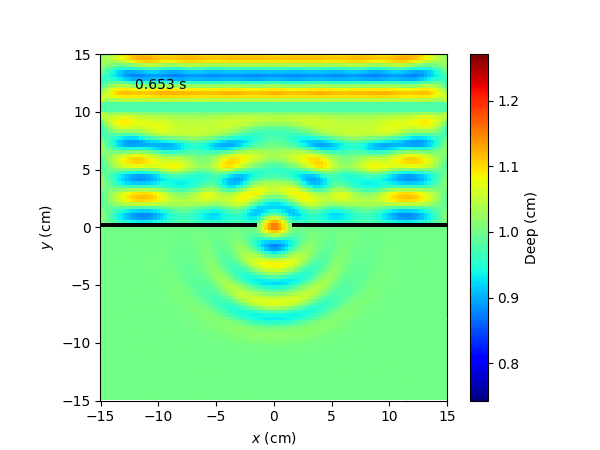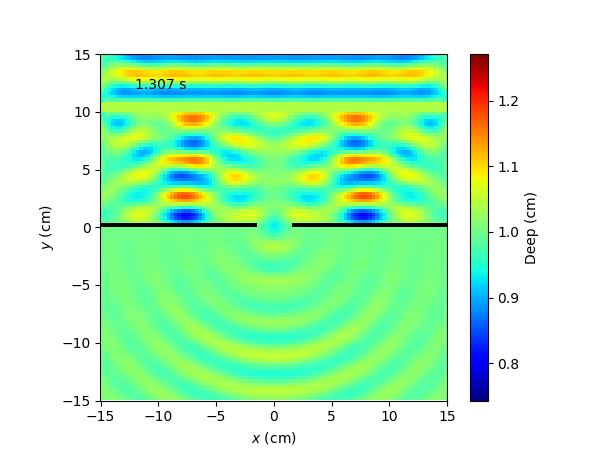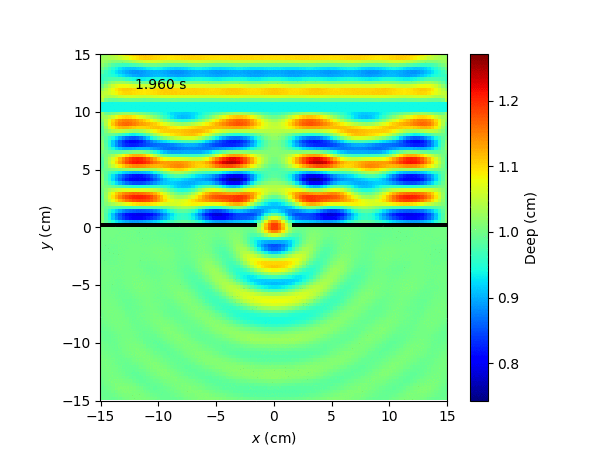
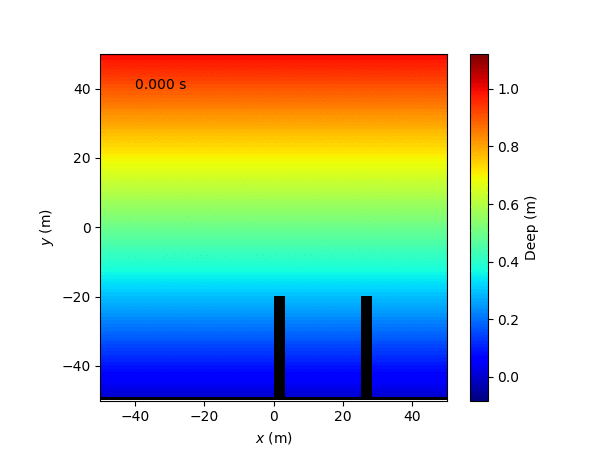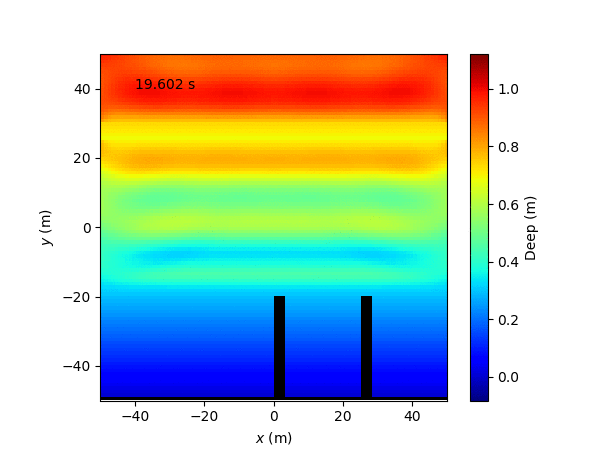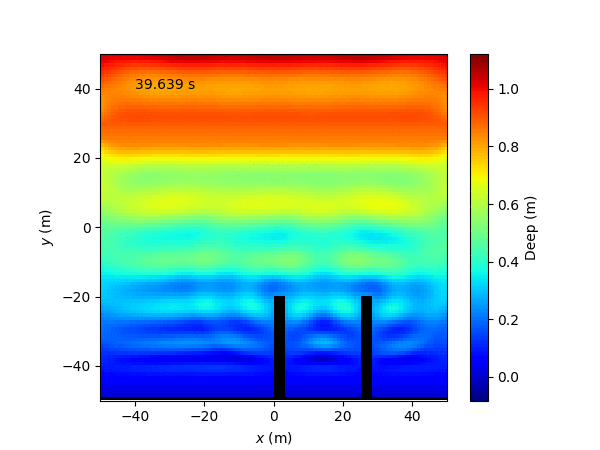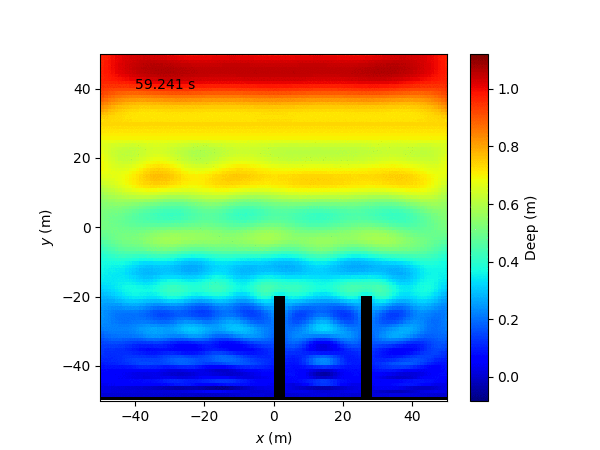
For a gaussian wave with open boundary conditions the result is:
Documentation¶
rippleTank is divided in four scripts: masks.py, sources.py, tank.py, examples.py. They contain the definition of three classes: Mask, Source and rippleTank.
Root class is rippleTank which defines the whole space in which the simulation will take place. Perturbations are included with Source objects and obstacules with Mask objects.